In man-caused catastrophes it is necessary to quickly detect the survivals among bricks or broken concrete slabs. The process of heartbeat, breathing and motion of human bodies is the distinctive sign of a living man. Selecting these signs is made possible by the Doppler analysis of radar echo signals. The level of the signals reflected from a targets is very low - (140.100) dB. Noises and coherent radar clutters result from the sounding signals reflection from walls, trees, human beings, cars etc.

The basic products of rescue-radars development are:

 a) video pulse radars [1 - 7];

 b) continuous-signal radars [8, 14, 15].

For continuous-signal radars is important to choose a signal, whose ambiguity function [9] would be near to the pencil (push-button) type. The level of side lobe of such a function must not exceed ‑ (100…70) dB. Phase ‑ coded manipulated signals [10, 14] at 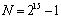 have the side lobes below ‑ 80 dB. The depth of signal penetration 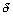 of in the bricks and concrete walls in accordance with 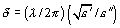 is directly proportional to the sounding signal wavelength. Under real condition the signal propagation environment is not homogeneous, since it may coming of wreckage, debris of broken concrete slabs etc. For example, 1 GHz signal propagating through a concrete wall 1 m thick decreases its energy by 40 dB. The losses of a 10 GHz signal are reducing by nearly 90 dB. Thus, the higher is the signal frequency, the easier is the signal penetration through metallic frames. And the lower is the signal frequency, the easier is it’s the signal penetration into the barriers. The optimum sounding signal frequency is within the limits of (1…2,5) GHz. The signal polarization must be circular for the increase the probability of penetration of sounding signal into the barriers.

The radiation power should exceed the receiver’s proper noise by 10 to 20 dB. Therefore the radar power is chosen from 100 to 150 mW with a receiver sensitivity of ‑ 170 dBW.

2. Block diagram of rescue-radar.

The generalized block diagram of the portable rescue-radar is shown in Fig. 1.

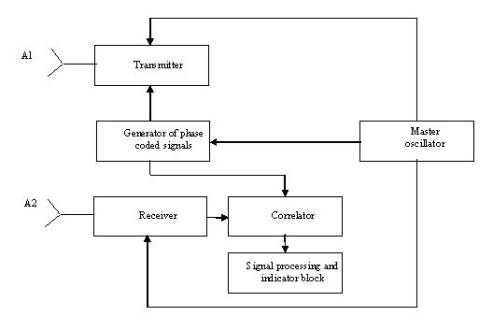
Fig.1 Generalized rescue-radar block diagram

The distinctive feature of the radar with a pseudorandom sounding signal is the need to form coherent modulating functions for the transmit-and-receive channels. Therefore a general high stability master oscillator with a relative instability of signal frequency 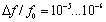 at a carrier frequency of 2 GHz is the basic element of the block diagram. From a signal of the master oscillator are formed: carrying signal of the transmitter; a basic signal heterodyne oscillator to the receiver; basic signal for the modulator; clock signals for the block of processing. The frequencies of all signals are generated either by division or multiplication of the master oscillator frequency. The automatic frequency control is not employed. In Fig. 2 the complete rescue-radar block diagram is shown. Radar is operated as follows. The output signal of master oscillator 1 simultaneously is fed to amplitude modulator 2 and two frequency dividers 3 and 4 with the division factors 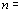20 and 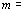10 respectively. At the other input of amplitude modulator 2 the 100 MHz oscillations are set up from divider 3. Narrow-band filters 8, 9 are connected to the output of modulator 2 serve to sort out oscillations of upper sideband (filter 8) and lower side band (filter 9). Separations of coherent oscillations frequencies at the outputs of filters 8 and 9 are 200 MHz. The upper sideband oscillations of are used in the radars transmitter to generate the sounding signal, and the lower side band oscillations are used to generate for the receivers heterodyne. A sounding signal in balanced modulator 7 is increased by amplifier 6 to the value -10 dBW and radiated by transmitting antenna 5 in space. The pseudorandom modulating function generated in block 10 has effected upon the other input of balanced modulator 7. The clock rate of the reference oscillator is generated from 1 by dividing the frequency in block 3. The pseudorandom function is generated in block 10 by a numerical procedure. The subcarrier frequency is 1,3 kHz. The subcarrier oscillation period is made equal to two periods of pseudorandom signal. Upon multiplying the required delays of the pseudorandom signal are formed in block 11 for range target selection. The receiver heterodyne signal appears at the balanced modulator 12 output. The coherent transmitter signal and pseudorandom signal are fed to the inputs of block 12 from filter 9 and block 10. The signals from the output of antenna 14 and amplified by amplifier 15, with a noise factor of 2 dB and amplifying factor of 10 to 15 dB are fed to the first input of balanced mixer 16 while the heterodyne signal from block 13 is fed to the second input of block 16 (correlator). Bandpass filter 17 is connected to the output of mixer 16. From the output of block 17 the signal at the intermediate frequency of 200 MHz is fed to two quadrature channels 18, 19. The information signal is transferred to a subcarrier frequency of 1,3 kHz in balanced mixers 20 of each channel. The quadrature signals are separated in each channel by means of phase shifter 27. These signals are filtered in bandpass filters 21 and amplified in narrow-band low-frequency amplifiers 22. These signals are then squared in blocks 23 and added in block 24. The decision-making concerning the presence or absence of a target is accomplished by block 26.

3. Signal processing.

The multiplicative unstationary process model can be thought of as some stochastic oscillations with the appropriate probabilistic laws. And at the same time, these processes have the saving properties of periodic repetition (heartbeat and breathing). Therefore we will build the informative process model at the Doppler radar output in terms of the class of models with multiplicative unstationarity. One of the most widespread methods of describing the multiplicative unstationarity processes is presented by the correlation function of the process of the form

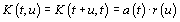 ,                                                      (1)

where 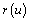 is the correlation function of the stochastic process, that meets the follow condition

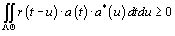                                                         (2)

With all complex 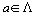, where 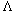 is the complex plane, all 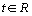, where 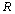 is the real axis, the symbol ^* denotes the complex conjugation.

It is evident that if the assumption about the slowness of function 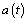 with respect to 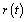 hold true, then an expression for the process dispersion can be written as

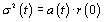 ,                                                              3)

where 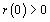 and, by definition, function 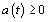 for all .

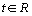Fig.1 Block scheme rescue-radar

Expression (2) given the convenient description of the model for the steady and multiplicative unsteady processes. Indeed, if 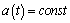, (3) determines the dispersion of the stationary process. It is obvious that the signals with correlation function of type (1) is to not exist in nature. It is strongly indicative in [11]. In fact, condition (2) holds, when a correlation function depends not only upon the specific values of 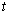 and 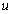 but upon their difference, i.e. 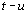: 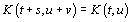. But in this case the must be a symmetric in relation to (1) correlation function 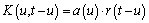. It is easy to show that for the process with involving the correlation function (1) impossible the hermitian symmetry condition, which consists of equality 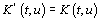. However, at 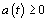 it is implement this equality. Therefore multiplier 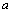 in expression for the correlation function of the real informative process must depend not only on 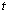 but also upon 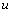, i.e.

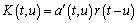 .                                                     (4)

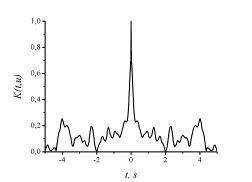
Model (4) is the one with unshared variables. This feature is well illustrated by experimental data. In Fig.3 the fragment of correlation function model of the informative process of the Doppler radar at the output normalized to the its maximum is shown. This function is calculated in the interval of 10 second. 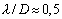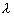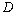This particular function is calculated from the echo signal backscattered from a human thorax at a 2,5 m distance to the target (the radar operating frequency is 1,8 GHz, ,  - is the wavelength,  is the aperture linear dimension).

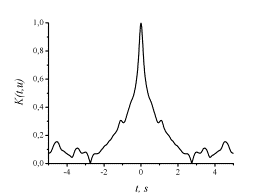
The fragment of the correlation function of that process, which is computed in the interval of 200 second is shown in Fig.4. The obvious differences in these functions are evidenced by the fact the variables in (4) are unshared. As well as for model (1), it is possible to define dispersion for a model (4).

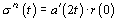 ,                                                         (5)

Comparing correlation (5) and (3) it is possible to write 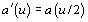, then model (4) has the form as

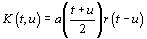  .                                                       (6)

In formula (6) both factors can now be expressed via one variable which is linear combination of two initial variables. Thus, (6) acquires a sufficiently clear physical meaning. So, the first factor can be regarded as the process dispersion in the middle of the time span between the two components, the correlation linkage between them being determined by the second factor. By replacing of variabl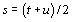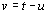es ,  we again obtain process model with the shared variables

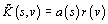.                                                                                                   (7)

Fig.3. Module of the correlation function calculated on the 10-second interval.	Fig. 4. Module of the correlation function calculated on the 200-second interval

However, the complete consistence of theoretical model (1), i.e. factorization of the correlation function here is not achieved. Lets us enter displacement in time, i.e.

  .                                                 (8)

It is evident, that in this case both the periodogram and correlogram spectral estimations of such processes will be unstationary in time. Traditionally the instantaneous values of spectral components of the informative process can be represanted on an interval 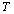, by direct Fourier-transformation

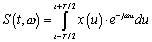,                                                        (9)

where 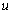 is the variable having with the time dimension; 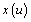 it is the realization of the process being observed.

The dependence of spectral model (5) upon the concrete moments of time makes this model inadequate. However, if the correlation function of the periodically correlated process [12] is used, then it is possible to construct a spectral time-independent model. Such a model is based on establishing the correlation between the separate spectral components, the so-called spectral-correlation function [13]

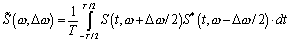  ,                                     (10)

where 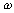 is the middle of frequency interval, and  is the frequency displacement with respect for .

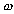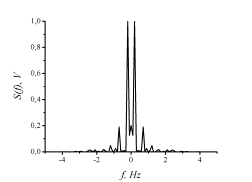
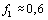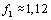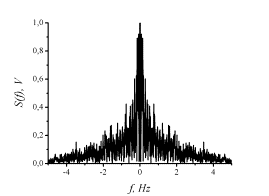
The module of the spectral-correlation function of the informative process calculated above is shown in Fig. 5. As seen from Fig.5 the components remaining from breathing (at a frequency  Hz and heartbeats at a frequency  of Hz) are clearly visible. For comparison the periodogram spectral density of this informative process is presented in Fig.6.

4. Conclusion.

 Thus, all the rescue radar signals must be absolutely coherent. In signal processing it is impossible to employ model (4) with incompletely shared variables. When synthesizing the algorithms for detecting recognizing and identifying objects it is necessary to make use of periodically correlated processes model is preferred. The rescue radar parameters are given in Table 1. 

Table 1.

The external view of the rescue radar is shown in Fig.6. Receive-ttansmitt antennas are incorporated in a single design. All radar blocks are placed in separate screened cells in the common design. The power supply batteries are placed in a separate shockproof bag. The power supply unit is coupled to the radar through a separate cable.